Introduction to Neural Networks(with Zero Knowledge)

👋 Welcome!

Have you ever wondered how machines recognize faces, translate
languages, or recommend your next favorite song? The magic behind many
of these applications is Neural Networks --- a key concept in machine
learning. In this blog post, we'll break down neural networks in the
simplest way possible and even build one from scratch in Python! ## 🧠
What Is a Neural Network?

Think of a neural network as a mini version of your brain, made up of
neurons that pass information to each other.

• It takes input data (like pixels of an image).
• Passes it through layers of neurons.
• And produces an output (like "cat" or "not cat").

Each neuron performs a simple math operation and passes the result to
the next layer. By adjusting how strongly neurons are connected (called
weights), the network "learns" patterns in data. Let's get started

1. Building Blocks: Neurons

A Simple Example

Just like our brain has billions of neurons, artificial neural networks
are made up of artificial "neurons" --- simple math units that process
data.

A neuron:

• Takes some inputs (e.g., numbers),
• Multiplies each by a weight,
• Adds a bias,
• Passes the result through an activation function.
  

3 things are happening here. First, each input is multiplied by a weight
(red box):

x 1 → x 1 ∗ w 1

x 2 → x 2 ∗ w 2

Next, all the weighted inputs are added together with a bias b (green
box):

( x 1 ∗ w 1 ) + ( x 2 ∗ w 2 ) + b

Finally, the sum is passed through an activation function:

y=f(x1∗w1+x2∗w2+b) > Formula

output=σ(w1x1+w2x2+⋯+wnxn+b)

Where:

• 𝑥ᵢ: input\
• 𝑤ᵢ: weight\
• 𝑏: bias\
• 𝜎: activation function (e.g., sigmoid)

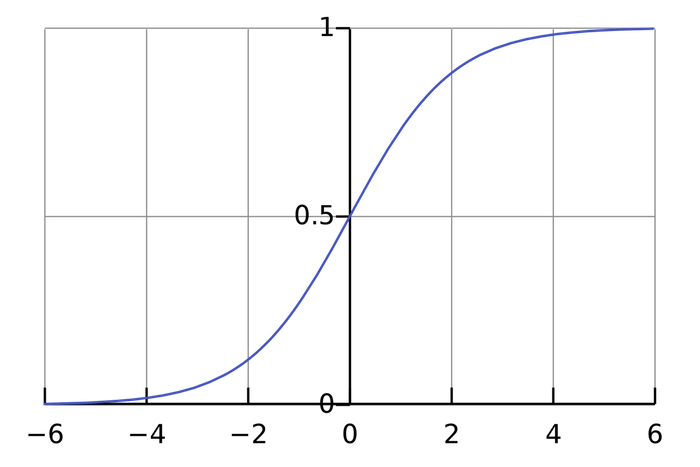
The activation function is used to turn an unbounded input into an
output that has a nice, predictable form. A commonly used activation
function is the Sigmoid
Function :

Coding a Neuron Let's write a simple Python function to simulate a

single neuron using the sigmoid activation function.

import numpy as np

def sigmoid(x):
    return 1 / (1 + np.exp(-x))

# Inputs
inputs = np.array([0.5, 0.3])
weights = np.array([0.4, 0.7])
bias = 0.2

# Output of the neuron
z = np.dot(inputs, weights) + bias
output = sigmoid(z)

print(f"Neuron output: {output:.4f}")

OR

import numpy as np

def sigmoid(x):
  # Our activation function: f(x) = 1 / (1 + e^(-x))
  return 1 / (1 + np.exp(-x))

class Neuron:
  def __init__(self, weights, bias):
    self.weights = weights
    self.bias = bias

  def feedforward(self, inputs):
    # Weight inputs, add bias, then use the activation function
    total = np.dot(self.weights, inputs) + self.bias
    return sigmoid(total)

weights = np.array([0, 1]) # w1 = 0, w2 = 1
bias = 4                   # b = 4
n = Neuron(weights, bias)

x = np.array([2, 3])       # x1 = 2, x2 = 3
print(n.feedforward(x))    # 0.9990889488055994

2. Combining Neurons into a Neural Network

Simple Feedforward Neural Network

A neural network is nothing more than a collection of neurons connected
together. Here's an example of a simple feedforward neural network:

• 2 input neurons
• 1 hidden layer with 2 neurons:
  • ( h_1 ) and ( h_2 )
• 1 output neuron:
  • ( o_1 )

Each neuron in one layer passes its output as input to the neurons in
the next layer. That's what makes this structure a network.

A hidden layer is any layer between the input and output layers.
Neural networks can have multiple hidden layers --- deep learning
typically involves many! ## An Example: Feedforward

Let's walk through an example using this network.

Assumptions

• All neurons share the same weights:
  ( w = [0, 1] )

• All biases are:
  ( b = 0 )

• Activation function is sigmoid:
  f(z)= 1/(1+e^-z)

• Input vector:
  ( x = [2, 3] )

Hidden Layer Calculation

Both ( h_1 ) and ( h_2 ) use the same weights and bias:

[ h_1 = h_2 = f(w.x + b) = f(0*2 + 1 * 3 + 0) = f(3) = 0.9526 ]

Output Layer Calculation

Now, the output neuron ( o_1 ) takes ( h_1 ) and ( h_2 ) as input:

[ o_1 = f(0.9526) = 0.7216 ]

✅ Final Output

For input ( x = [2, 3] ), the output of the network is:

[ o_1 = 0.7216 ]

Coding Simulation

You could include a simple code snippet like this to let readers test
the output:

import numpy as np

def sigmoid(x):
    return 1 / (1 + np.exp(-x))

# Inputs
x = np.array([2, 3])
w = np.array([0, 1])
b = 0

# Hidden layer
z_hidden = np.dot(w, x) + b  # Same for h1 and h2
h = sigmoid(z_hidden)

# Output layer
w_output = np.array([0, 1])
o_input = np.dot(w_output, [h, h]) + b
output = sigmoid(o_input)

print("Output:", output)  # Should be ~0.7216

OR

import numpy as np

# ... code from previous section here

class OurNeuralNetwork:
  '''
  A neural network with:
    - 2 inputs
    - a hidden layer with 2 neurons (h1, h2)
    - an output layer with 1 neuron (o1)
  Each neuron has the same weights and bias:
    - w = [0, 1]
    - b = 0
  '''
  def __init__(self):
    weights = np.array([0, 1])
    bias = 0

    # The Neuron class here is from the previous section
    self.h1 = Neuron(weights, bias)
    self.h2 = Neuron(weights, bias)
    self.o1 = Neuron(weights, bias)

  def feedforward(self, x):
    out_h1 = self.h1.feedforward(x)
    out_h2 = self.h2.feedforward(x)

    # The inputs for o1 are the outputs from h1 and h2
    out_o1 = self.o1.feedforward(np.array([out_h1, out_h2]))

    return out_o1

network = OurNeuralNetwork()
x = np.array([2, 3])
print(network.feedforward(x)) # 0.7216325609518421