Problem Statement: Arranging Coins

You have n coins and you want to build a staircase with these coins. The staircase consists of k rows where the ith row has exactly i coins. The last row of the staircase may be incomplete.

Given the integer n, return the number of complete rows of the staircase you will build.

Example 1:

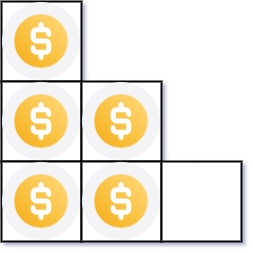
Input: n = 5
Output: 2
Explanation: Because the 3rd row is incomplete, we return 2.

Example 2:

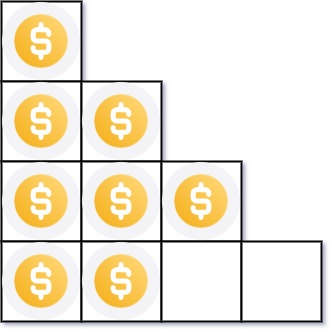
Input: n = 8
Output: 3
Explanation: Because the 4th row is incomplete, we return 3.

Constraints:

1 <= n <= 2^31 - 1
.
.
.
.
.
Try it Yourself (Hint: Do You Know Binary Search)
.
....If not ,refer to :Binary Search
.
.
.
.
.
Fun Fact: The problem of arranging coins to form a staircase is linked to triangular numbers and even has a playful nickname—the "Pyramid Scheme" of coins.
.
.
.

Solution:

// using cpp

#include <iostream>
using namespace std;

int arrangeCoins(int n) {
    long long left = 0, right = n, mid, curr;
    
    while (left <= right) {
        mid = (right + left) / 2;
        curr = mid * (mid + 1) / 2;
        
        if (curr == n)
           return mid;
        if (curr < n) {
            left = mid + 1;
        } 
        else {
            right = mid - 1;
        }
    }
    
    return right;
}

int main() {
    int n;
    cout << "Enter the number of coins: ";
    cin >> n;
    cout << "Number of complete rows: " << arrangeCoins(n) << endl;
    return 0;
}

Explanation:

• Binary Search: The code uses a binary search approach to efficiently find the maximum number of complete rows.

• Mid Calculation: For each mid value, it calculates the sum of the first mid natural numbers.

• Comparison: It compares this sum to n to adjust the search range until the correct number of rows is found.